Julia-带有事件的微分方程
我们将以椭圆台球为例. 假设台球是由以下曲线所围成的:
其中 为大于 的实数. 质点自由运动的方程即是
现在有了微分方程. 我们还需要写出事件. 事件由某个关于状态变量以及时间的函数零点给出. 自然地, 事件发生的条件即是
现在我们定义了事件. 接下来需要定义事件发生后, 微分方程的状态是如何改变的. 假设碰撞发生的坐标为 , 质点的速度为 . 不妨设此时的单位外法线为 . 那么碰撞后的速度为:
下面我们就给出具体的程序实现.
using DifferentialEquations, LinearAlgebra, Plots
const a, b = 2, 1
function f(du, u, p, t) # 状态变量分布为 x,x',y,y'
du[1] = u[2]
du[2] = 0
du[3] = u[4]
du[4] = 0
end
function condition(u, t, integrator) # 定义事件发生为函数的零点
u[1]^2 / a^2 + u[3]^2 / b^2 - 1
end
function normal(u) # 单位外法线方向
normalize([2 * u[1] / a^2, 2 * u[2] / b^2])
end
function affect!(integrator) # 定义事件发生时系统的状态如何改变
state = integrator.u # 得到碰撞时系统的状态
integrator.u[2], integrator.u[4] = state[[2, 4]] - 2 * (dot(state[[2, 4]], normal(state[[1, 3]]))) * normal(state[[1, 3]])
end
cb = ContinuousCallback(condition, affect!, save_positions=(false, true)) # save_positions 第一个问是否保持事件发生前的状态, 第二个问是否保存事件发生后的状态
u0 = [0.0, 1.0, 0.0, 1.2] # 初值
timespan = (0.0, 100.0) # 积分区间
prob = ODEProblem(f, u0, timespan) # 定义 ODE 方程
sol = solve(prob, Tsit5(), callback=cb, save_everystep=false, save_start=false, save_end=false) # 求解事件的 ODE 方程, 不保存任一个积分点, 这样只有事件发生时的状态得到储存
function third(u)
u[3]
end
function para(s)
[a * cos(s), b * sin(s)]
end
plot(first.(sol.u), third.(sol.u), color=:black, axis=([], false), legend=false) # 画出质点轨迹
data = para.(0:0.01:2pi)
plot!(first.(data), last.(data), color=:black) # 再画出椭圆如上程序将会产生如下漂亮的图片: 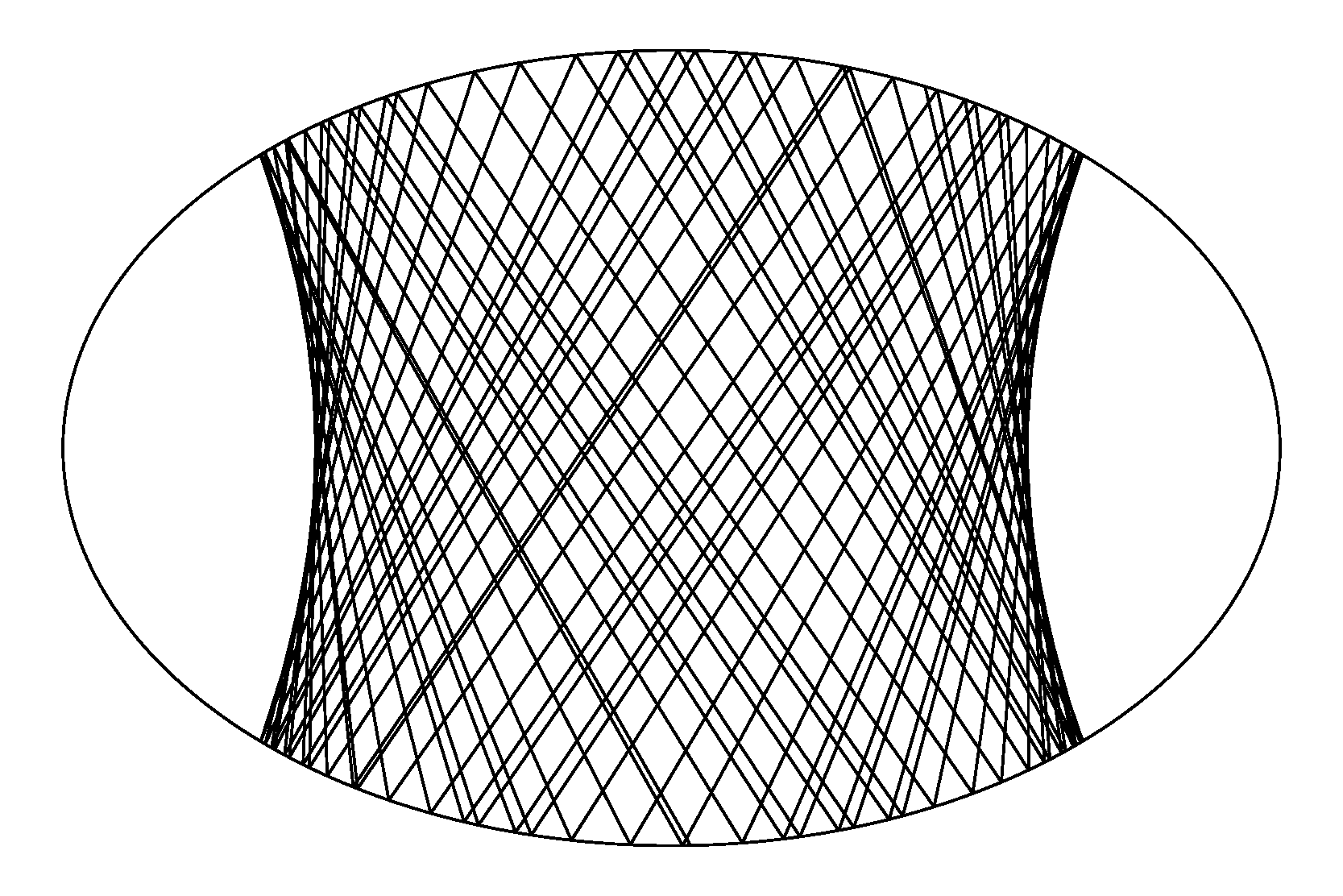
Website built with Franklin.jl and Julia.