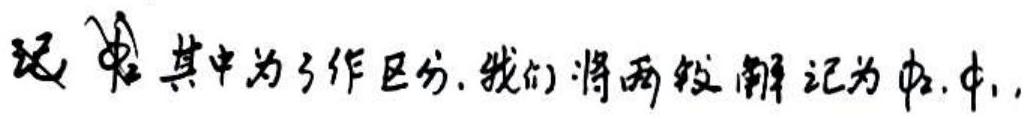基解矩阵作为时间推进映射的导数, 其基本性质与计算方法对于研究周期解的分出与稳定性是王关重要的.
考虑 n 阶非自治系统:
x˙=f(x,t).(1) 其中 x∈R2,t∈R,f:R2xRarrowRn 是 C2 类矢量场, 假没 ∀(t0,γ0) , 存在唯一解 ϕ(t,t0,x0),t∈R.
给定 t0,t1∈R, 定义时间推进晎射:
ϕ:x0↦ϕ(t1,t0,x0),ψ(t1,t0)(x0)=ϕ(t1,t0,x0).dψ(t1,t0)(x0)=Φ(t1,t0)(x0)=ϕx0(t1,t0,x0).
由定义, Φ(t1,t0)(x0) 即时间推进映射的导数(在 x0 处).
定理 1. 时间推进映射在x0处的导数 Φ(t1,t0)(x0) 是以下初值问题的解:
x˙=fx(ϕ(t,t0,y0),t)x,x(t0)=I.(2) 其中 X 为 n×n 的矩阵, I 为单位矩阵.
证明: 由 ϕ(t,t0,x0) 满足(1), 代入并对x0求导得到
ϕ˙x0(t,t0,x0)=fx(ϕ(t,t0,x0),t)ϕx0(t,t0,x0). 即.
dtdϕx0(t,t0,x0)=fx(ϕ(t,t0,x0),t)ϕx0(t,t0,x0). 由 ϕ(t0,t0,x0)=x0.ϕx0(t0,t0,x0)=I. 故 ϕγ0(t,t0,x0)=Φ(t,t0)(x0) 是 (2) 的解.
一般地, 称 (u)为解 ϕ(t1,t0)(x0) 的变分方程, 这个变分方程的解称作是基解矩阵. 这里我们强调 Φ(t1,t0)(x0) 其作为时间推进映射的导数这一特性.
下面的定理给出了Φ(t1,t0)的性质.
定理 2
Φ(t,t0)=Φ(t,t1)Φ(t,t0).
若 f(x,t)=f(x) 不依赖于时间, 则 Φ(t,t0)=Φ(t−t,0) , 且有
f(ϕ(t1,x0))=Φ(t0)(x0)f(x0),∀t∈R,x0∈Rn. 证明, 利用 ϕ(t1,t0,x0)=ϕ(t,t1,ϕ(t1,t0,x0)) , 井对x0求导即得到 1).
同样, 若 f 不依赖于时间, 那么由 ϕ(t,t0,x0)=ϕ(t−t0,0,x0), 即可得到 2) 的第一条结论.
由于 ϕ(t,0,ϕ(s,0,x0))=ϕ(s,0,ϕ(t,0,x0)) , 在 t=0 处求得到
.ϕ˙(t,0,ϕ(s,0,x0))∣t=0=f(ϕ(s,0,γ0))=.ϕx(s,0,ϕ(t,0,x0))ϕ˙(t,0,x0)∣t=0=ϕx(s,0,y0)f(x0), 即 Φ(s,0)(x0)f(x0)=f(ϕ(s,0,x0)), 特别地, 若 ϕ(t0,0,x0)=x0 .则
Φ(t0,0)(x0)f(x0)=f(x0), 即 f(x0) 是 Φ(t0,0)(x0) 1 特征值对应的特征矢量.
接下来我们考虑如何计算分段光滑系绕时间推进映射的导数, 首先这个映射需要具有可微性才谈得上导般这一概念, 一段地可通过假设流的横藏性来确保其可微性.
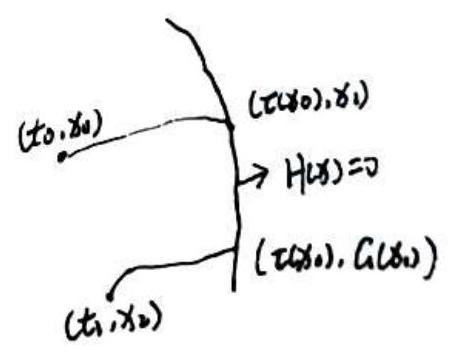
考虑如下分段光滑系统:
{x˙=f1(x,t),x˙=f2(x,t),H(x)<0H(x)>0(3) 其中, f1,f2 为 C2 类失量场, H:RnarrowR 是 C1 类乎数, 对 y∈{x:H(x)=0} , 要求 dH(0)=0 , 即 {x:H(x)=0}是 Rn 中的一个超曲面. 记 (3), (4) 的流分别为 ϕ1,ϕ2 .
设 (*) 的一个解 ϕ(t,t0,x0∗) 满足:
{H(ϕ1(t,t0,x0∗))<0,t∈[t0,t~0)H(ϕ2(t,t~0,ϕ1(t,t0,x0∗)))>0,t∈(t~0,t1]  以及一个 c′ 类数 τ:UarrowR , 使得 x0∈U 时有
以及一个 c′ 类数 τ:UarrowR , 使得 x0∈U 时有
.H(ϕ1(τ(x0),t0,x0))=0.dH(ϕ1(τ(x0),t0,x0))ϕ˙1(τx0),t0,x0)=0. 定义时间推进映射
ϕ:UarrowR.x0↦ϕ(t1,t0,x0)=ϕ2(t1,τ(x0),ϕ1(τ(x0,t0,x0)).. 下湍我们来计算中的导数. 引理1. 设 n(x) 为 H(x) 的单位法短, 即 dH(x)=∣dH(x)∣n(x)⊤ , 那么我们肉
dτ(x0)=−⟨n,f1⟩n⊤ϕ1x0, 其中 n=n(ϕ1(τ(x0),t0,x0)),ϕ1x0=∂x0∂ϕ1(τ(x0),t0,x0),f1=f1(ϕ1(τ(x0),t0,x0),τ(x0)).
证昒:由 .H(ϕ1(τx0),t0,x0))=0 , 关于 γ0 求导得到
dH(ϕ˙1dτ(x0)+ϕ1x0)=0,arrowdτ(x0)=−dHϕ˙1dHϕ1x0=−n⊤f1n⊤ϕ1x0. 引理工.设 x˙=f(x,t) 的解为 ϕ(t,t0,x0),ϕ(t0,t0,x0)=x0 .则 ∂t0∂ϕ(t) 地, .x0)(t
∂t0∂ϕ(t,t0,x0)=−∂x0∂ϕ(t,t0,x0)f˙(x0,t0). 证明: 对 ϕ(tt0,x0)=ϕ(t,t0+s,ϕ(t0s,t0,x0)) 关于s在 s=0 处求导得到
d=∂t0∂ϕ(t,t2+s,ϕ(t0+s,t0,x0)),.ϕ˙(t0+s,t0,x0)∣x00=0=.∂t0∂ϕ(t,t0+s,ϕ(t0+s,t0,x0))∣s=0+.∂x0∂ϕ(t,t0+s,ϕ(t,+s,t0,x0))ϕ˙(t0+s,t0,x0)∣s=0=∂t0∂ϕ(t,t0,x0)+∂x0∂ϕ(t,t0,x0)f˙(x0,t0) 为简洁起便, 对于在分界面处取值的短及西数不再写出括号内的量.
定理了.
dη=Φ2(t1,τ(x))SΦ1(τ(x),t0)(x0) , 其中 S=I+(f2−f1)⟨n⋅f1⟩n⊤⋅Φ2,Φ1 分别为(4)(3)的基解矩阵
证明: dx0d(ϕ2(t1,τ(x0),ϕ1(τ(x0),t0,γ0)))=∂t0∂ϕ2dτ(x0)+∂x0∂ϕ2(ϕ˙1(τ(x0),t0,x0)dτ(x0)+∂x0∂ϕ1)
=−∂x0∂ϕ2f2⋅(−⟨n1f1⟩n⊤ϕx0)+ϕ2x0(f1(−⟨n1f1⟩n⊤ϕ1x0+ϕ1x0).=ϕ2γ0(I+(f2−f1)⟨n1f1⟩n⊤)ϕ1x0, 其中我们用到了引理 1 , 2 .
 且若 ⟨n,f2⟩=0 , S是非化的.
且若 ⟨n,f2⟩=0 , S是非化的.
S−1=1+(f1−f2)⟨n,f2⟩n⊤. 当东㟋(*)容许在超平面 {x:H(x)=0} 存在滑移轨线, 此时矩阵S是退化的.实际上, 伤类似先前的推导, 若 f2 的短场不在 {x:H(x)<0} 而在 {x:H(x)=0} 上, 仍可得到
dp=Φ2(t1,τ(x))SΦ1(τ(x),t0),S 的表达式完全一样, 不过此时有 ⟨n,f˙2⟩=0 . 命题1: 若 f2 定文在 {x:H(x)=0} , 则 S 的核由 f2−f1 张成.
证明: 由 ⟨n,f˙2⟩=0,S(f2−f1)=f2−f1+(f2−f1)⟨n1−f1⟩n⊤(f2−f1)=0.
而一个形如 I+ ab⊤ 的特姃值为 {1+b⊤a,1,⋯,1} .
多 abb=⟨n1f1⟩f2−f1,b=n , 得到 b⊤a=−1 , 故 S 仅有一个 0 特征值.
注: 对于矩阵 I+ab⊤( 设 a,b=0) , 与 b 正交的聜间的基 3u1,⋯,un+3 构成了其n-1个1相应的特征生量.
又 (I+ab⊤)a=a+ab⊤a=a(1+b⊤a)=(1+b⊤a)a , 故 a 是 1+b⊤a 对应的特征奭.
命题1解释了Filippov系统周期解为行总出现一个0
 般化此问题.
般化此问题.
考虑来统 x˙=f(x,t) .
设来统存在一个起曲面 {x:H(x)=0} , 以及一个保持此曲的
不变的映射 a , 即 y∈{x:H(x)=0} , 则有 H(G(y))=0 .
系绕的轨线碰到曲面 {x:H(x)=0} 后, 其状态作如下安化:
(t1,x1)↦(t1,G(x1)), 条
假没轨线不在曲面 {x:H(x)=0} 停留, 即 ⟨dH⊤,f(x1(t1)⟩=0,⟨dH⊤,f(x2,t1)⟩=0. . 类似地, 可定义 τ(x) 以及晎时
ψ:x0↦ϕ2(t1,τ(x1),G(ϕ1(τ(x1),t0,x0))). 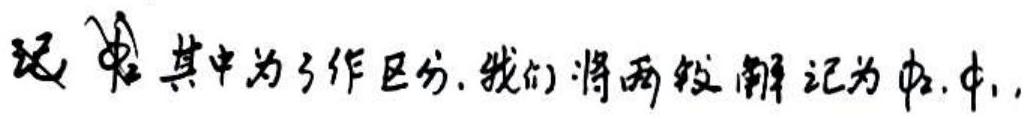
定理4.
dη=Φ2(t1,τ(tx0))(⟨n,ϕ˙1⟩ϕ˙2n⊤−dGϕ˙1n⊤+dG)Φ1(τ(x0),t0). 证明:
==.dx0dϕ2(t1,τ(x0),G(ϕ1(τ(x0),t0,x0)))=∂t0∂ϕ2dτ(x0)+ϕ2x0dG(ϕ˙1dτx0)+ϕ1x0)−ϕ2x0ϕ˙2(−⟨n,ϕ˙1⟩n⊤ϕ1x0)+ϕ2x0dG(ϕ˙1−⟨n,ϕ˙1⟩n⊤ϕ1x0+ϕ1x0)ϕ2x0(⟨n,ϕ˙1⟩ϕ˙2n⊤−dGϕ˙1n⊤+dG)ϕ1x0. 例, 设系统为
{x˙=yy˙=g(x,y,t). H(x,y)=0,G(x,y)=(x,−ry) .设碰撞点为 (x∗,y∗,t∗) , 则
ϕ˙1=(y∗g(x∗,y∗,t∗)),ϕ˙2=f(G(x∗,y∗),t∗)=(−ry∗g(x∗,−r∗,t∗)),n=(1,0)⊤,dG=(100−r) 此时:
⟨n,ϕ˙,ϕ2˙n⊤−daϕ˙1r⊤+da=y∗1((−r∗g(x∗,−ry∗,t∗.)(1,0)−(100−r)(y∗g(x∗,y∗,t∗.)(1,0))+(100−γ)=(−γy∗1(g(x∗,+y∗,t∗)+rg(x∗,y∗,t∗))0−γ)
 以及一个 类数 , 使得 时有
以及一个 类数 , 使得 时有 且若 , S是非化的.
且若 , S是非化的. 般化此问题.
般化此问题.